
Détail de la fractale de Mandelbrot
Comme expliqué sur ma page d'accueil, je suis en math' spé, au lycée Pissarro. C'est la deuxième année de prépa. Elle se termine par les concours qui nous permettent d'intégrer une grande école d'ingénieurs (Polytechnique ou Centrale pour les meilleurs).
Une des épreuves que nous avons au concours est le TIPE. Une partie de cette épreuve est la présentation, devant un jury, d'un travail de recherche effectué pendant l'année. Nous avons la liberté de choisir le sujet qui nous intéresse, à condition qu'il corresponde. Cette année, le thème est : « Limite - Stabilité - Variabilité ».
Comme vous le savez sûrement, j'aime beaucoup explorer et étudier les fractales mathématiques. Voici la définition que donne Benoît Mandelbrot des fractales :
Fractale : n. f. Ensemble mathématique ou objet physique fractal.
Fractal : adj. Sens intuitif. Se dit d'une figure géométrique qui combine les caractéristiques que voici. A) Ses parties ont la même forme ou structure que le tout, à ceci près qu'elles sont à une échelle différente et peuvent être légèrement déformées. B) Sa forme est soit extrêmement irrégulière, soit extrêmement fragmentée quelle que soit l'échelle d'examen. C) Il contient des « éléments distinctifs » dont les échelles très variées couvrent une très large gamme.
Source : MANDELBROT, Benoît. « Lexique de néologismes ». In Les objets fractals. Paris : Flammarion, 1995 (4ème édition). p. 154
La plupart de celles que vous pouvez observer dans ma galerie sont construites par une méthode relativement simple :

Quelle conclusion pouvons-nous tirer de cela ? Simplement que le sujet des fractales est parfaitement adapté au thème de cette année, puisque c'est l'étude de l'instabilité des limites de suites. C'est même un sujet type. Dans le cadre de ces TIPE, je vais donc étudier des fractales, parce que ça me passionne, et parce que c'est parfaitement dans le sujet.
Oui, mais voilà : les fractales, c'est un thème assez vaste. Il faut donc trouver un angle d'attaque pour ce sujet. De plus, je ne peux pas me contenter simplement de lire les études faites par Benoît Mandelbrot ou Gaston Julia, puis ressortir le tout lors de l'oral. Il faut surtout, comme l'épreuve le demande, que je fasse un travail de recherche, si possible accompagné d'un travail de programmation (dans le cadre des fractales, ça ne doit pas être très difficile à faire).
Les fractales n'ayant connues un réel essor que depuis une trentaine d'années, il reste encore pas mal de chose à découvrir. Après tout, pourquoi ne pas découvrir une nouvelle fractale ? Ça ne doit pas être trop difficile, c'est un excellent thème, je pourrais probablement en faire une étude approfondie, et le travail de programmation peut être celui de l'intégrer à un logiciel déjà existant (au hasard, GNU/XaoS). Il ne me restait plus qu'à trouver la fractale.
Très rapidement, l'idée m'est venue d'utiliser une double-suite. C'est à dire d'étudier l'évolution de 2 suites en parallèle, chaque suite étant définie récursivement en fonction des 2 termes précédents. J'ai repensé à une exercice que l'on avait fait (l'année dernière ou celle d'avant), qui consistait à étudier un tel système de suites. La première était la moyenne arithmétique des deux termes, la seconde était la moyenne harmonique de ces termes. Dans tous les cas, cette suite convergeait vers une certaine valeur. Ce n'était donc pas assez intéressant pour en faire une fractale.
Mon imagination m'a suggéré d'étudier un système de suites assez proche : la première suite est la moyenne des deux termes précédents, la seconde est le produit de ces termes. Cela donne, mathématiquement :
Pour ces suites, on peut définir deux paramètres : u0 et v0.
Il est intéressant de constater que les suites ainsi définies peuvent l'être sur n'importe quelle algèbre. Pour rester dans des limites raisonnables, je vais me limiter à R et C pour le moment. Pour chaque espace, on nomme « Béryl » (ou B, indicé par le nom de l'ensemble) l'ensemble des valeurs initiales pour lesquelles la paire suite converge. Par exemple, pour R, BR est une partie de R2.
Dans le plan cartésien, on peut décider de « colorier » chaque point en fonction de la convergence (ou non) du système de suite, dont les valeurs initiales seront l'abscisse et l'ordonnée du point. Ainsi, pour un point M (x, y), si le système de suite défini précédemment avec les valeurs u0 = x et v0 = y ne converge pas vers 0, on décide de noircir (ou colorier) le point. On sait que si la valeur absolue de deux termes est strictement inférieure à 1, alors les suites convergent toutes deux vers 0 (les preuves viendront plus tard, quand j'aurais le courage de tout convertir en LaTeX). On sait que la droite d'équation y = x sera un axe de symétrie de la figure, puisque les rôles de x et y sont symétriques.
Cette représentation crée une figure en forme de « neurone », avec de grosses synapses le long des axes, et des synapses moins grosses en-dehors de ces axes. On comprend, intuitivement, d'où viennent ces synapses : pour une valeur u0 ou v0 suffisamment « petite » (proche de 0), la valeur suivante de la suite v sera aussi assez petite. Si la suite v reste suffisamment longtemps proche de 0, alors la suite u convergera vers 0 (terme presque divisé par à chaque étape), et les deux termes seront, à un moment, compris entre 0 et 1.
De même, on peut s'intéresser aux conditions pour qu'un des termes devienne nul (dans ce cas, le système converge forcément vers (0,0)). Pour que vn soit nul, il vaut que vn-1 ou un-1 soit nul. Pour qu'un terme de la suite u s'annule, il faut que les deux termes précédents soient opposés. La droite d'équation y = -x sera donc le support d'une des synapses, tous les points sur cette droite représentent des valeurs pour laquelle la suite converge.
Pour aller plus loin, on peut s'intéresser aux antécédents de ces valeurs (termes opposés). Pour une valeur T donnée (T réel non compris entre -1 et 0), les antécédents du couple de valeurs (-T, T) est le couple de valeurs :
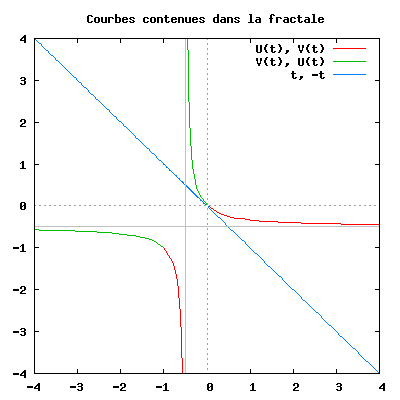
Graphiquement, on constate que les courbes paramétrées par ces deux fonctions sont bien dans la figure. Ces courbes sont représentée à droite (source GNUplot) : on constate qu'elles ont pour asymptotes les droites d'équation x = -0.5 et y = -0.5 (représentées en traits pleins sur la figure). En conséquence, en plus des branches le long des axes des abscisses et des ordonnées, on a aussi des branches le long de ces axes. Intuitivement, on peut comprendre pourquoi : prenons un très grand nombre. La moyenne de ce nombre et de -1/2 sera environ égale à la moitié de ce nombre Le produit de ce nombre et de -1/2 sera lui égal à l'opposé de la moitié du nombre choisi. Mathématiquement, la preuve peut se faire en utilisant un changement de variable, puis par le théorème des gendarmes (pour prouver que la fonction issue du changement de variable tend vers 0 quand t tend vers l'infini positif ou négatif).
Il est très probable que, à la frontière entre la région dans laquelle la suite converge vers 0 et la région ou la suite diverge, il y ait des points particuliers pour lesquels, par exemple, la suite converge vers une valeur finie ou a un comportement cyclique. La seule valeur évidente, à mes yeux, est le couple (1, 1). Pour ces valeurs initiales, le système sera constant, les deux termes étant égaux à 1. Le seul antécédent de ce couple de valeur par notre système de suite est ce couple lui-même.
On peut, de manière assez aisée, montrer que si, pour un rang n donné, la valeur absolue (ou, dans C, le module) du terme vn est supérieur à trois fois la valeur absolue de un, et que cette dernière valeur absolue est elle-même supérieur à 2, alors ces deux conditions restent vérifiées pour les termes suivants de la suite. Dans ce cas, on peut dire que la suite diverge.
Si l'on considère C2 comme un espace vectoriel réel (ce qui est le plus simple pour pouvoir représenter les fractales), alors la forme est de dimension 4. Il est donc impossible de la représenter directement sur un écran (de dimension 2) ou de le façonner physiquement (on aurait une figure de dimension 3). En conséquence, il va falloir observer des projections de BC, et des projections sur un plan si nous voulons pouvoir les observer à l'écran.
La première chose que l'on remarque, c'est que BR est un ensemble de dimension 2 incluse dans BC. En effet, de manière évidente, si la suite converge pour une paire de valeurs réelles dans l'ensemble des réels, elle converge de la même façon dans l'ensemble des complexes. BR est donc une projection particulière de Béryl complexe. Mais on peut définir une inifité d'autres projections.
Pour une valeur u0 donnée, on étudie le comportement de la suite pour les valeurs v0 (représentés dans le plan). Intuitivement, je sais qu'il existera des valeurs pour lesquelles ces suites convergeront vers 0, d'autres pour lesquelles la suite divergera. Par exemple, pour deux nombres u0 et v0 différents de module inférieur ou égal à 1, les suites vont tendre vers 0.
La représentation d'une telle fractale sur calculette donne, la plupart du temps, une figure comprenant une patatoïde contenant l'origine du repère. Pour certaines valeurs, il y a plusieurs patatoïdes, distinctes de la première. Une fois, je suis tombé sur une sorte de « goutte d'eau » (une forme contenant deux « têtes », rétrécie entre les deux) : c'était pour la valeur -0.49, en zoomant sur 24.5 (à 10-6 près).
À l'aide d'outils informatiques adaptés, on peut représenter cette fractale. On aperçoit effectivement, parfois, des formes en gouttes d'eau. On observe aussi d'autres propriétés intéressantes (non prouvées, donc pas forcément exactes dans tous les cas) :
Ces propriétés sont à formaliser mathématiquement et à démontrer. Ce ne sont que des conjectures, pour le moment.
J'ai essayé de programmer en logo l'affichage de cette fractale. Les paramètres sont définis en début de programme. Il est fait pour être interprété par UBCLogo. Malheureusement, ceci étant mon premier programme Logo, il ne fonctionne pas et est très mal codé. Alors si vous avez des compétences en logo, et que vous souhaitez m'aider, n'hésitez pas à jeter un oeil. Le message d'erreur est, actuellement : « I don't know how to true in while ».
Ce programme est sensé représenter l'étude du système pour une paire de réels (u0 en abscisse, v0 en ordonnée).
J'ai réalisé un patch pour GNU/XaoS qui permet de tracer les deux fractales. Actuellement, le seul bogue concerne l'aperçu quand on explore les valeurs complexes, il ne fonctionne pas comme il faut. Pour l'utiliser, il faut que vous téléchargiez les sources de GNU/XaoS, que vous copiiez le patch dans le dossier, puis que vous y tapiez la commande « patch -p0 < formulas.c.patch ». Cela fait, il ne vous reste plus qu'à compiler le programme selon la procédure habituelle habituelle, décrite dans les README et autres INSTALL (./configure && make && ./bin/xaos suffit, normalement). Les fractales se nomment Beryl, Emeraude, Heliodor et Aquamarine, accessibles par les raccourcis Maj+O, P, Q ou R. Par contre, leur nom n'étant pas encore définitif, les fichiers .xpf que vous enregistrerez avec cette version modifiée de GNU/XaoS ne seront pas compatibles avec la version suivante, qui inclura éventuellement ces fractales.
NB : Je décline toute responsabilité en cas de dommages liés aux opérations décrites ci-dessus. Vous pouvez tester, vous en êtes libres, mais c'est à vos risques et périls. Ne le faites pas si vous ne savez pas ce que vous faites.
C'est beau ? Même moi qui suis intimement convaincu de la subjectivité de la notion de « beau », je suis forcé d'admettre que les formes définies par ces suites ne sont pas très agréables à observer. Vous pouvez l'observer par vous-même sur ces images (calculées à partir de la version modifiée de GNU/XaoS). Cependant, je trouve que, d'un point de vue mathématique, elles sont intéressantes. D'abord par leurs propriétés et par leur structure fractale : ces formes qui apparaissent à peu près régulières sont, en réalité, très complexes, cachent énormément de détails qu'un examen rapide ne permet pas de visualiser. Ensuite, ce qu'elles représentent me semble toucher à la base de tous nos raisonnements. Les opération élémentaires, parmi les nombres usuelles, sont le produit et la somme. Ces fractales sont directement liées à ces deux simples opérations. Elles représentent un peu la « forme graphique » de l'association des opérations « moyenne » et « produit ». C'est passionnant de se dire que tout ce qui régit les lois physiques de notre monde est présent derrière ces images.
Je n'ai jamais eu écho de l'existence d'une étude sur un tel système de suites. Si cela existe déjà, merci de me prévenir, cela m'éviterait un travail inutile et me permettrait de changer assez tôt d'angle d'attaque sur le sujet.
Ce document est signé : signature.
Le document est publié sous licence CC-BY-SA. Vous pouvez le copier, le modifier ou en utiliser des extraits, à condition de placer vos travaux dérivés sous une licence compatible, et de citer l'auteur (faire un lien vers cette page suffit).
Les morceaux de code contenus dans les fichiers annexes (« fichiers sources ») sont publiés sous licence GPL, version 3. Les droits accordés sont sensiblement les même.